
Unions and Intersections of Sets
- Introduction
- The Axiom of Pairing
- Unions of Sets
- Intersections of Sets
- The Complement of a Set
- The Power Set of a Set
- The Axiom of Foundation
- Notes and References
- Download
Introduction
In the following you will find a short summary of this unit. For detailed information please see the full text or download the pdf document at the end of this page.
The present unit is the second unit of the walk The Axioms of Zermelo and Fraenkel. In the first unit, The Mathematical Universe, we have introduced the first axioms of Zermelo and Frankel.
We will explain the following axioms of Zermelo and Fraenkel:
- ZFC-4: The Axiom of Pairing
- ZFC-5: The Axiom of Unions
- ZFC-6: The Axiom of Powers
- ZFC-7: The Axiom of Foundation
You will learn the meaning of the following terms:
The main results of this unit are
- Theorem [#nst-th-x-notin-x] excluding some strange constellations like $A \in A$ and
- de Morgan’s Laws (Theorem [#nst-th-de-morgan]) about the the complement of the union and the intersection of two sets.
The Axiom of Pairing
The axiom of pairing allows the creation of the new sets $\{A\}$ and $\{A, B\}$ provided that the sets $A$ and $B$ already exist:
Axiom. (ZFC-4: Axiom of Pairing) Let $A$ and $B$ be two sets.
(a) There exists the set ${\cal C} := \{ A \}$.
(b) There exists the set ${\cal D} := \{ A, B \}$.
French / German. Axiom of Pairing = Axiome de la paire = Paarmengenaxiom.
Theorem. (a) Let $A$ be a set. Then we have $A \notin A$.
(b) Let $A$ and $B$ be two sets. If the set $A$ is an element of the set $B$, then the set $B$ is no element of the set $A$.
(c) Let $A$ and $B$ be two sets. If the set $A$ is a subset of the set $B$, then the set $B$ is no element of the set $A$.
Unions of Sets
We need a proper axion, namely the axiom of unions, for the existence of the union of arbitrary many sets:
Axiom. (ZFC-5: Axiom of Unions) Let ${\cal C}$ be a set. Then there exists a set $U$ consisting of the elements $x$ that are contained in at least one element of the set ${\cal C}$, that is,
$$
x \in U \mbox{ if and only if there exists an element $C$ of the set ${\cal C}$ such that } x \in C.
$$
Axiom of unions = Axiome de la Réunion = Vereinigungsaxiom.
Definition. (a) Let ${\cal C}$ be a set, and let $U$ be the set consisting of the elements $x$ that are contained in at least one element of the set ${\cal C}$. The set $U$ is called the union of the set ${\cal C}$.
The set $U$ is denoted by
$$
U := \bigcup_{C \in {\cal C}} C \: \mbox{ or, equivalently, by } U := \bigcup \{ C \mid C \in {\cal C} \}.
$$
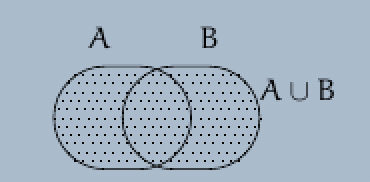
(b) If the set ${\cal C} = \{A, B\}$ consists of two sets $A$ and $B$, then we write $U := A \cup B$.
French / German. Union = Réunion = Vereinigungsmenge.
Note that it follows from the axiom of unions that the set $U := \bigcup_{C \in {\cal C}} C$ exists for all sets ${\cal C}$.
Intersections of Sets
The existence of the intersection of arbitrary many sets can be deduced from the axiom of specification introduced in Unit The Mathematical Universe. A proper axiom is not necessary.
Proposition. Let $\emptyset \neq {\cal C}$ be a non-empty set. Then there exists a set $D$ consisting of the elements $x$ that are contained in all elements of the set ${\cal C}$, that is,
$$
x \in D \mbox{ if and only if } x \in C \mbox{ for all } C \in {\cal C}.
$$
Definition. (a) Let $\emptyset \neq {\cal C}$ be a non-empty set. The set $D$ consisting of the elements $x$ that are contained in all elements of the set ${\cal C}$ is called the intersection of the set ${\cal C}$.
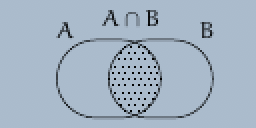
(b) The set $D$ is denoted by
$$
D := \bigcap_{C \in {\cal C}} C \: \mbox{ or, equivalently, by } D := \bigcap \{C \mid C \in {\cal C} \}.
$$
(c) If the set ${\cal C} = \{A, B\}$ consists of two sets $A$ and $B$, then we write $D := A \cap B$.
French / German. Intersection = Intersection = Durchschnitt.
Remark. In opposite to the union of sets, the empty intersection ($\cap_{C \in {\cal C}} C$ with ${\cal C} = \emptyset$) is not defined.
Proposition. Let $A$, $B$ and $C$ be three sets.
(a) We have
$$
(A \cup B) \cap C = (A \cap C) \cup (B \cap C).
$$
(b) We have
$$
(A \cap B) \cup C = (A \cup C) \cap (B \cup C).
$$
Definition. (a) Two sets $A$ and $B$ are called disjoint if their intersection is empty, that is, if we have $A \cap B = \emptyset$.
(b) If $A$ and $B$ are two disjoint sets, then we denote their union $U := A \cup B$ by $U = A \mathbin{\dot{\cup}} B$.
French / German. Disjoint = Disjoint = Disjunkt.
The Complement of a Set
The main result of this section is de Morgan’s Law which describes the complement of the union and the complement of the intersection of two sets:
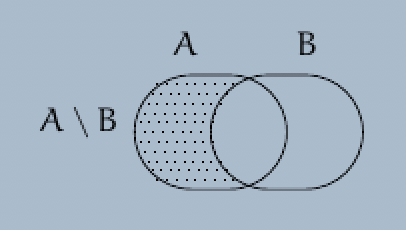
Definition. (a) Let $A$ and $B$ be two sets, and let $D := \{ x \in A \mid x \notin B \}$ be the set of the elements of the set $A$ which are not contained in the set $B$.
(b) The set $D$ is called the difference between the sets $A$ and $B$ or, equivalently, the complement of the set $B$ in the set $A$.
(c) The set $D$ is denoted by $A \setminus B$.
French / German. Complement = Complément = Komplement.
Theorem. De Morgan’s Laws Let $A$ be a set. For each subset $B$ of the set $A$, let $B^c := A \setminus B$ denote the complement of the set $B$ in the set $A$.
(a) We have $(X \cup Y)^c = X^c \cap Y^c$ for all subsets $X$ and $Y$ of the set $A$.
(b) We have $(X \cap Y)^c = X^c \cup Y^c$ for all subsets $X$ and $Y$ of the set $A$.
The Power Set of a Set
The axiom of power guarantees the existence of the set of all subsets of a given set:
Axiom. (ZFC-6: The Axiom of Powers) Let $X$ be a set. Then the set of all subsets of the set $X$ exists.
French / German. The Axiom of Powers = Axiome de l’ensemble des parties = Potenzmengenaxiom.
Definition. Let $X$ be a set. Then the set of all subsets of the set $X$ is called the power set of the set $X$. It is denoted by ${\cal P}(X)$.
French / German. Power set = Ensemble des parties d’un ensemble = Potenzmenge.
The Axiom of Foundation
The axiom of foundations excludes some strange constellations like $A \in A$:
Definition. Let $A$ be a set. An element $a$ of the set $A$ is called element minimal with respect to the set $A$ or, equivalently, $\in$-minimal with respect to the set $A$ if we have $a \cap A = \emptyset$.
French / German. Element minimal = Élément minimal pour l’appartenance = Element-minimal
Axiom. (ZFC-7: Axiom of Foundation) Every non-empty set $A$ contains an element $a$ which is element minimal with respect to the set $A$, that is, an element $a$ such that $a \cap A = \emptyset$.
French / German. Axiom of Foundation = Axiome de fondation = Fundierungaxiom.
Notes and References
A list of textbooks about set theory is contained in Unit [Literature about Set Theory].
Do you want to learn more? The next step is the definition of the direct product of two sets and the definition of relations. Of particular importance are equivalence relations. You will find all this in Unit Direct Products and Relations.
Download
Unions and Intersections of Sets
The pdf document is the full text including the proofs.
Current Version: 1.0.3 from October 2020
