Introduction into the Axiomatics of Zermelo and Fraenkel
Introduction
This walk can be understood as the entrance into the mathematical garden: We will explain the axiomatic foundation of mathematics based on the theory of sets as it has been developed by Ernst Zermelo, Abraham Fraenkel, Richard Dedekind, Georg Cantor and others.
There are two main objectives of this walk:
1. We want to invite you to explore the axiomatics of Zermelo and Fraenkel and to learn how the fundamental mathematical notions such as direct products, relations, functions, families of sets, order relations and equivalence relations are defined in a purely set-theoretical approach.
2. We will explain how the set $\mathbb{N}_0$ of the natural numbers can be formally defined based on the axiomatics of Zermelo and Fraenkel. This shows on the one hand the power of the concept and gives on the other hand an answer to the question why $3 +4 = 4 + 3$ or more generally why
$$
m + n = n + m \mbox{ for all natural numbers } m \mbox{ and } n.
$$
The walk The Axiomatics of Zermelo and Fraenkel consists of the following units:
The Mathematical Universe
We will explain in this unit that the mathematical universe consists of sets and nothing else. For that purpose you may explore the first axioms of Zermelo and Franekel, namely:
ZFC-0: The Basic Axiom
ZFC-1: The Axiom of Extension
ZFC-2: The Axiom of Existence
ZFC-3: The Axiom of Specification
ZFC-4: The Axiom of Foundation
The basic axiom states that every mathematical object is a set and that for each two sets $A$ and $B$ we either have $A \in B$ or $A \notin B$.
The axiom of extension explains when two sets $A$ and $B$ are equal. It says that
$$
A = B \mbox{ if and only if } A \subseteq B \mbox{ and } B \subseteq A.
$$
Most of the remaining axioms are needed to construct new sets from already existing sets. To do so, there must be at least one set: The axiom of existence guarantees that we have at least one set, namely the empty set $\emptyset$.
The construction of subsets of a given set $A$ is organized by the axiom of specification: It is a very strong axiom guaranteeing the existence of all subsets $B$ of a given set $A$ of the form
$$
B = \{ x \in A \mid \varphi(x) \}
$$
where $\varphi(x)$ is some mathematical property. For example, if $\varphi(x)$ denotes the property $x^2 \in C$ for a set $C$, then the subset
$$
B = \{ x \in A \mid \varphi(x) \} = \{ x \in A \mid x^2 \in C \}.
$$
of the set $A$ exists.
A somewhat surprising result is that the axiom of specification implies for each set $A$ the existence of an element (a set) $x$ such that $x \notin A$. In other words, there is no set containing all sets of our mathematical universe.
At the end of this unit you will learn about the rather technical axiom of foundation excluding some strange cases like $A \in A$ or $A \in B$ and $B \in A$ at the same time.
Unions and Intersections of Sets
So far we have ensured that there is at least one set (the empty set) and that for each set $A$ all subsets of the set $A$ which can be described by a mathematical property $\varphi(x)$, that is, alll subsets of the form
$$
B = \{ x \in A \mid \varphi(x) \}
$$
exist. As a next step we need some axioms which construct new sets from already existing sets. These axioms are
ZFC-5: The Axiom of Pairing
ZFC-6: The Axiom of Unions
ZFC-7: The Axiom of Powers
The axiom of pairing says that given two sets $A$ and $B$ there always exist the sets $\{ A \}$ and $\{ A, B \}$. This axiom ensures for example the existence of the sets $\{ \emptyset \}$ and $\big\{ \emptyset, \{ \emptyset \} \big\}$.
The axiom of unions starts with a set ${\cal A}$ of sets and guarantees the existence of the set

$$
\bigcup_{X \in {\cal A}} X := \{ x \mid \exists \: X \in {\cal A} \mbox{ such that } x \in X \}
$$
called the union of the sets of the set ${\cal A}$.
If ${\cal A} = \{ A, B \}$ for two sets $A$ and $B$, then we have
$$
A \cup B :=\bigcup_{X \in {\cal A}} X = \{ x \mid x \in A \mbox{ or } x \in B \}.
$$
Finally, the axiom of powers provides the existence of the set
$$
{\cal P}(A) := \{ X \mid X \subseteq A \}
$$
consisting of the set of all subsets of a given set $A$. The set ${\cal P}(A)$ is called the power set of the set $A$. If $A = \{a, b\}$, then we have
$$
{\cal P}(A) = \big\{ \emptyset, \{ a \}, \{ b \}, \{ a, b \} \big\}.
$$
In addition, we explain the concept of the intersection of sets
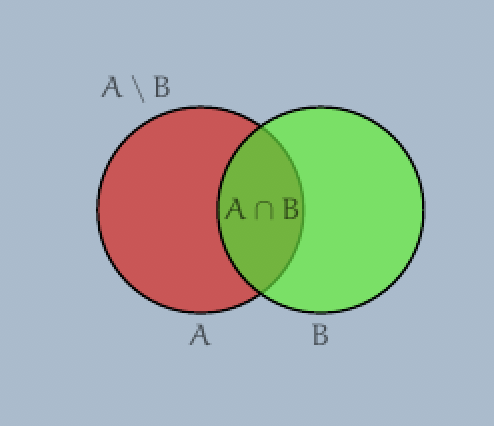
$$
\bigcap_{X \in {\cal A}} X := \{ x \mid x \in X \mbox{ for all } X \in {\cal A} \}
$$
and of the complement $A \setminus B$} defined by
$$
A \setminus B := \{ x \in A \mid x \notin B \}.
$$
Direct Products and Relations
Based on the Axioms ZFC-0 to ZFC-7 introduced so far we are able to define the direct product
$$
A \times B := \{ (a, b) \mid a \in A \mbox{ and } b \in B \}
$$
of two sets $A$ and $B$. Direct products are of fundamental importance in mathematics: For example, they are used to define the real plane
$$
\mathbb{R}^2 = \mathbb{R} \times \mathbb{R} = \{ (x, y) \mid x, y \in \mathbb{R} \}.
$$
In the context of the axiomatics of Zermelo and Fraenkel another aspect of the direct product is more important: The direct product allows to define a relation $R$ on the set $A \times B$ as a simple subset
$$
R \subseteq A \times B.
$$
The meaning is that an element $a$ of the set $A$ is related to the element $b$ of the set $B$ if and only if we have
$$
(a, b) \in R.
$$
Particularly important relations are functions, equivalence relations and order relations (see below).
An equivalence relation on a set $A$ is a relation
$$
R \subseteq A \times A
$$
which is normally denoted by $\sim$ and which has the following properties:
Reflexivity: $x \sim x$ for all $x \in A$.
Symmetry: $x \sim y$ implies $y \sim x$ for all $x, y \in A$.
Transitivity: $x \sim y$ and $y \sim z$ imply $x \sim z$ for all $x, y, z \in A$.
A familiar example of equivalence relations is illustrated by the equation
$$
\frac{1}{2} = \frac{2}{4}.
$$
Of course, the pairs $(1, 2)$ and $(2, 4)$ are different. Defining two pairs $(a, b)$ and $(c, d)$ to be equivalent if $ad = bc$, the pairs $(1, 2)$ and $(2, 4)$ become equivalent which is the formal basis for the above equation.
You will find a detailed explanation of the equivalence sets in Unit Direct Products and Relations.
Functions and Equivalent Sets
In the axiomatics of Zermelo and Fraenkel a function $f : A \rightarrow B$ is also a special sort of sets, namely a relation
$$
f \subseteq A \times B
$$
with the property that for each element $x$ of the set $A$ there exists exactly one element $y$ of the set $B$ such that $(x, y) \in f$. In other words, we have $y = f(x)$.
In the unit we will regain the familiar description of a function $f$ as a mapping
$$
f : A \rightarrow B
$$
from a set $A$ into a set $B$. However, this exact definition of a function is very helpful when proving the existence of certain functions. You will see interesting examples in the unit.
Fundamental properties of functions are the terms injective, surjective and bijective. You will find a detailed explanation in the unit.

Families and the Axiom of Choice
In this unit you will encounter the next two axioms:
ZFC-8: The Axiom of Substitution
ZFC-9: The Axiom of Choice
The axioms of Zermelo and Fraenkel provide strict rules about the existence of sets. Therefore we also have to explain what a family $\big( A_i \big)_{i \in I}$ means and under which conditions such families exist. In this context we need a further axiom, namely the axiom of substitution. Roughly speaking, it says the following:
Suppose that for each element $i$ of an index set $I$, the set $B_i$ exists. For example, we can think of an already existing family $\big( A_i \big)_{i \in I}$ and of a further set $C$. Then, by the axiom of unions, the set $A_i \cup C$ exists for each element $i$ of the set $I$. The axiom of substitution guarantees the existence of the family $\big( B_i \big)_{i \in I}$ with
$$
B_i := A_i \cup C \mbox{ for all } i \in I.
$$
You will find a more detailed explanation in the corresponding unit.
After the definition of the families and the introduction of the axiom of substitution we will explain how to apply the concepts union, intersection, direct product and complement to families of sets.
The concept of families also allows the definition of direct products of arbitrary many sets, more precisely of families of sets in the form
$$
\prod_{i \in I} A_i.
$$
Finally, at the end of this unit, we will explain the axiom of choice. It says that if $\big( A_i \big)_{i \in I}$ is a family of non-empty sets, then the direct product $\prod_{i \in I} A_i$ is also non-empty. Another way to express this axiom is to say that for each family $\big( A_i \big)_{i \in I}$ of non-empty sets $A_i$ there exists a function
$$
f : \{ A_i \mid i \in I \} \rightarrow \bigcup_{i \in I} A_i
$$
such that
$$
f(A_i) \in A_i \mbox{ for all } i \in I.
$$
In other words, we may choose an element $x_i := f(A_i)$ of the set $A_i$ for each element $i$ of the set $I$. This sounds quite obvious, but it is not.
Ordered Sets and the Lemma of Zorn
A familiar example of an order is the relation
$$
1 \leq 2 \leq 3 \leq \ldots
$$
on the set of the natural numbers. In this unit we will explain that a (partial) order $\leq$ on a set $A$ is a relation on the set $A$ with the following properties:
Reflexivity: $x \leq x$ for all $x \in A$.
Antisymmetry: $x \leq y$ and $y \leq x$ imply $x = y$ for all $x, y \in A$.
Transitivity: $x \leq y$ and $y \leq z$ imply $x \leq z$ for all $x, y, z \in A$.
Note that we will distinguish between a partial order and a total order: A totally ordered set $A = (A, \leq)$ has the property that
$$
x \leq y \mbox{ or } y \leq x \mbox{ for all } x, y \in A,
$$
that is, any two elements of the set $A$ can be compared. The standard order $\leq$ on the set of the natural (or the real) numbers is an example of a total order. For a partially ordered set we have the situation that there may exist two elements $x$ and $y$ such that neither $x \leq y$ nor $y \leq x$. The power set ${\cal P}(A)$ of a set with at least two elements together with the order $\subseteq$ is an example. If $A = \{ 1, 2, 3 \}$, then we neither have
$$
\{ 1, 2 \} \subseteq \{ 2, 3 \} \mbox{ nor } \{ 2, 3 \} \subseteq \{ 1, 2 \}.
$$
Wherever we have to deal with ordered sets, maximal elements will play an important role. The famous and important Lemma of Zorn says that if $A$ is a (partially) ordered set with the property that every totally ordered subset of the set $A$ admits a maximal element, then the set $A$ has a maximal element.
Successor Sets and the Axioms of Peano
The axioms of Peano are not part of the axioms of Zermelo and Fraenkel. They have been introduced earlier by Giuseppe Peano as an axiomatic system for the definition of the natural numbers. Starting with the axioms of Zermelo and Fraenkel we are able to prove the axioms of Peano, so the axioms of Peano become the Theorem of Peano.
To do so, we need the last of the axioms of Zermelo and Fraenkel, namely
ZFC-10: The Axiom of Infinity
It is more or less identical to Axiom (P5) of Peano. It guarantees the existence of an infinite set which is necessary to construct the natural numbers. It says:
There exists a set ${\cal A}$ with the following properties:
(i) The empty set $\emptyset$ is contained in the set ${\cal A}$.
(ii) If the set $A$ is contained in the set ${\cal A}$, then the set $A^+ := A \cup \{ A \}$ is also contained in the set ${\cal A}$.
By the way, the set $A^+ := A \cup \{ A \}$ is called the successor of the set $A$. In the rest of the unit we will explain how this set ${\cal A}$ can be used to construct a so-called Peano set, that is a set fulfilling the axioms of Peano mentioned above. This Peano set will be used to give a formal definition of the set of the natural numbers.
The Natural Numbers and the Principle of Induction
In the last unit we will show the strength of the axiomatics of Zermelo and Fraenkel by giving a formal definition of the natural numbers: We will set
$$
0 := \emptyset, \: 1 := \{ 0 \} = \{ \emptyset \}, \: 2 := \{ 0, 1 \} = \big\{ \emptyset, \{ \emptyset \} \big\}, \ldots
$$
The definition of the first natural numbers is of course possible without the axiom of infinity. The axiom of infinity is needed to construct the set
$$
\mathbb{N}_0 := \{ 0, 1, 2, 3, \ldots \}
$$
of all natural numbers.
After their introduction we will explain how to define the operations
$$
m + n, \: m \cdot n \mbox{ and } m^n \mbox{ for all } m, n \in \mathbb{N}_0
$$
and how to define the natural order $\leq$ on the set $\mathbb{N}_0$ such that
$$
0 \leq 1 \leq 2 \leq 3 \leq \ldots
$$
One big advantage of this axiomatic approach is the fact that we are now able to prove the arithmetical laws like the commutativity of the addition or the multiplication. All this will be explained in detail.
The main tool for all of these proofs is the principle of induction which turns out to be a theorem (with a proof) and not to be an abstract proof method which has to be believed without further justification.
The introduction of the natural numbers concludes the first walk through the mathematical garden.
