
Ordered Sets and the Lemma of Zorn
- Introduction
- Ordered Sets
- Isomorphisms of Ordered Sets
- Initial Segments
- Chains of Ordered Sets
- The Lemma of Zorn
- Notes and References
- Download
Introduction
In the following you will find a short summary of this unit. For detailed information please the full text or download the pdf-document at the end of this page.
The present unit is the sixth unit of the walk The Axioms of Zermelo and Fraenkel. We will explain the concept of (partially) ordered sets. The main result of this unit is the Lemma of Zorn about the existence of maximal elements.
You will learn the meaning of the following terms:
- Order Relation
- Partially and Totally Ordered Sets
- Induced Order
- Chain in an Ordered Set
- Minimum or Minimal Element
- Maximum or Maximal Element
- One Point Extension of a Set
- Homomorphism, Monomorphism, Epimorphism, Isomorphism and Automorphism of Ordered Sets
- Isomorphic Ordered Set
- Automorphism Group of an Ordered Set
- Initial Segment
- Final Segment
- Chains of Ordered Set
- Order induced by the Orders of a Chain of Ordered Sets
The main results are
- Theorem [#nst-th-extension-bijective-function-to-union] about the possibility to extend functions $f_i : A_i \rightarrow B_i$ form ordered sets into ordered sets to a common function $f : \bigcup_{i \in I} A_i \rightarrow \bigcup_{i \in I} B_i$,
- Theorem [#nst-th-isomorphism-ordered-sets-subgroup-functions] saying that the automorphism group of an ordered set $A$ is a subgroup of the group ${\cal B}(A)$ of the bijective mappings from the set $A$ onto itself,
- Theorem [#nst-th-ordered-chain-order-union] allowing to transfer the orders of a chain $(A_i, \leq_i)_{i \in I}$ of ordered sets to an order $\leq$ of the set $\bigcup_{i \in I} A_i$ and
- the Lemma of Zorn about the existence of maximal elements in partially ordered sets.
Ordered Sets
We will explain the concept of ordered sets. Minimal and maximal elements are of particular importance when studying ordered sets.
Definition. Let $A$ be a set, and let $R$ be a relation on the set $A$.
(a) The relation $R$ is called an order or, equivalently, a partial order on the set $A$ if it fulfills the following conditions:
(i) The relation $R$ is reflexive, that is, $x R x$ for all elements $x$ of the set $A$.
(ii) The relation $R$ is antisymmetric, that is, $x R y$ and $y R x$ imply $x = y$ for all elements $x$ and $y$ of the set $A$.
(iii) The relation $R$ is transitive, that is, $x R y$ and $y R z$ imply $x R z$ for all elements $x$, $y$ and $z$ of the set $A$.
(b) A partial order is often denoted by $\subseteq$ or by $\leq$.
(c) A set $A$ with a (partial) order $R$ or $\leq$ is called an ordered set or, equivalently, a partially ordered set and is often denoted by $A = (A, R)$ or by $A = (A, \leq)$.
(d) Two elements $x$ and $y$ are called comparable with respect to the order $\leq$ if we have $x \leq y$ or $y \leq x$.

(e) A (partial) order $\leq$ on a set $A$ is called a total order if we have $x \leq y$ or $y \leq x$ for all elements $x$ and $y$ of the set $A$. A set $A$ with a total order $\leq$ is called a totally ordered set.
French / German. (Partially) Ordered Set = Ensemble (partiellement) ordonné = (Partiell) geordnete Menge. Totally ordered set = Ensemble totalement ordonné = Vollständig geordnete Menge.
Definition. Let $A = (A, \leq_A)$ be an ordered set, let $B$ be a subset of the set $A$, and let $\leq_B$ be the order on the set $B$ such that
$$
x \leq_B y \mbox{ if and only if } x \leq_A y \mbox{ for all } x, y \in B.
$$
The order $\leq_B$ is called the order on the set $B$ induced by the order $\leq_A$.
Often we write $A = (A, \leq)$ and $B= (B, \leq)$ without explicitly distinguishing between the order $\leq_A$ on the set $A$ and the induced order $\leq_B$ on the set $B$.
French / German. Induced order = Ordre induit = Induzierte Ordnung.
Definition. A subset $C$ of an ordered set $A = (A, \leq)$ is called a chain if the subset $C = (C, \leq)$ is totally ordered with respect to the order induced by the order of the set $A$. In particular, a totally ordered set is a chain.
French / German. Chain = Chaîne = Kette.
Definition. Let $A = (A, \leq)$ be an ordered set, and let $a$ and $b$ be two elements of the set $A$.
(a) Set $a < b$ if $a \leq b$ and $a \neq b$.
(b) Set $a \geq b$ if $b \leq a$.
(c) Set $a > b$ if $a \geq b$ and $a \neq b$, that is, if $b < a$.
Definition. Let $A = (A, \leq)$ be an ordered set, and let $B$ be a subset of the set $A$.
(a) An element $b$ of the set $B$ is called a maximal element or a maximum of the set $B$ if we have
$x \leq b$ for all $x \in B$ comparable to $b$.
Note that the element $b$ (if it exists) is contained in the set $B$.
(b) An element $b$ of the set $B$ is called a minimal element or a minimum of the set $B$ if we have
$b \leq x$ for all $x \in B$ comparable to $b$.
Note that the element $b$ (if it exists) is contained in the set $B$.
French / German. Maximum = Maximum = Maximum. Minimum = Minimum = Minimum. Maximal element = Élément maximal = Maximales Element. Minimal element = Élément minimal = Minimales Element.
Definition. Let $A = (A, \leq_A)$ be an ordered set, and let $b$ be an element not contained in the set $A$. Set $B := A \mathbin{\dot{\cup}} \{ b \}$. We define an order $\leq_B$ on the set $B$ as follows:
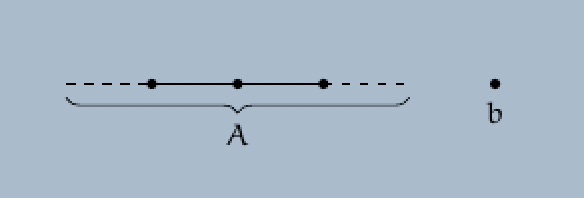
For each two elements $x$ and $y$ of the set $A$, set $x \leq_B y$ if and only if $x \leq_A y$. For each element $x$ of the set $B$, set $x \leq_B b$.
The pair $(B, \leq_B)$ is called the one point extension of the pair $(A, \leq_A)$.
French / German. The notion one point extension is probably no standard notion in mathematics. It is based on the notion one-point compactification of Alexandroff. I am not aware of a corresponding French expression. One point extension = Einpunkt-Erweiterung.
Theorem. Let $I$ be a totally ordered index set, and let $(A_i)_{i \in I}$ and $(B_i)_{i \in I}$ be two families of sets with the following properties:
(i) The families $(A_i)_{i \in I}$ and $(B_i)_{i \in I}$ are chains, that is, we have
$$
A_i \subseteq A_j \mbox{ and } B_i \subseteq B_j \mbox{ if } i \leq j.
$$
(ii) For each element $i$ of the set $I$, there exists a function $\alpha_i : A_i \rightarrow B_i$ from the set $A_i$ into the set $B_i$.
(iii) For each two elements $i$ and $j$ of the set $I$ such that $i \leq j$ the function $\alpha_i : A_i \rightarrow B_i$ is induced by the function $\alpha_j : A_j \rightarrow B_j$, that is, we have
$$
\alpha_i(x) = \alpha_j(x) \mbox{ for all } x \in A_i.
$$
Let
$$
A := \bigcup_{i \in I} A_i \mbox{ and } B := \bigcup_{i \in I} B_i.
$$
(a) There exists exactly one function $\alpha : A \rightarrow B$ from the set $A = \bigcup_{i \in I} A_i$ into the set $B =\bigcup_{i \in I} B_i$ such that $\alpha|_{A_i} = \alpha_i$ for all elements $i$ of the set $I$.
(b) If the functions $\alpha_i : A_i \rightarrow B_i$ are injective for all elements $i$ of the set $I$, then the function $f : A \rightarrow B$ is also injective.
(c) If the functions $\alpha_i : A_i \rightarrow B_i$ are surjective for all elements $i$ of the set $I$, then the function $f : A \rightarrow B$ is also surjective.
(d) If the functions $\alpha_i : A_i \rightarrow B_i$ are bijective for all elements $i$ of the set $I$, then the function $f : A \rightarrow B$ is also bijective.
Remark. Theorem [#nst-th-extension-bijective-function-to-union] allows to replace the functions $\alpha_i : A_i \rightarrow B_i$ by one function $\alpha : A \rightarrow B$.
Isomorphisms of Ordered Sets
We explain the isomorphisms between ordered sets:
Definition. Let $(A, \leq_A)$ and $(B, \leq_B)$ be two ordered sets, and let $\alpha: A \rightarrow B$ be a function from the set $A$ into the set $B$.
(a) The function $\alpha: A \rightarrow B$ is called a homomorphism of ordered sets if we have
$$
x \leq_A y \mbox{ implies } \alpha(x) \leq_B \alpha(y) \mbox{ for all } x, y \in A.
$$
A homomorphism of ordered sets is also called a homomorphism if no danger of confusion arises.
(b) An injective homomorphism $\alpha: A \rightarrow B$ is called a monomorphism of ordered sets.
(c) A surjective homomorphism $\alpha: A \rightarrow B$ is called an epimorphism of ordered sets.
(d) A bijective homomorphism $\alpha: A \rightarrow B$ with the property that the inverse function $\alpha^{-1} : B \rightarrow A$ is also a homomorphism is called an isomorphism of ordered sets.
(e) The ordered sets $(A, \leq_A)$ and $(B, \leq_B)$ are called isomorphic if there exists an isomorphism $\alpha: A \rightarrow B$ from the set $A$ onto the set $B$. If the sets $A$ and $B$ are isomorphic, then we write $A \cong B$.
(f) An isomorphism $\alpha: A \rightarrow A$ from the set $A$ onto itself is called an automorphism of the set $A$
French / German. Homomorphism = Homomorphisme (or morphisme) = Homomorphismus. Monomorphism = Monomorphisme = Monomorphismus. Epimorphism = Épimorphisme = Epimorphismus. Isomorphism = Isomorphisme = Isomorphismus. Automorphism = Automorphisme = Automorphismus.
Theorem. Let $(A, \leq)$ be an ordered set, and let
$$
{\cal B}(A) := \{ f : A \rightarrow A \mid f \mbox{ is bijective} \}.
$$
Then the set ${\rm Aut}(A)$ of the automorphisms of the set $A$ is a subgroup of the group ${\cal B}(A)$.
Definition. Let $(A, \leq)$ be an ordered set, and let $G$ be the group of the automorphisms of the set $A$ (Theorem [#nst-th-isomorphism-ordered-sets-subgroup-functions]).
(a) The group $G$ is called the full automorphism group of the ordered set $(A, \leq)$. It is denoted by ${\rm Aut}(A)$.
(b) Every subgroup of the group $G$ is called an automorphism group of the ordered set $(A, \leq)$.
French / German. Automorphism group of an ordered set = Groupe d’automorphismes d’un ensemble ordonné = Automorphismengruppe einer geordneten Menge.
Initial Segments
Initial segments will play an important role in the study of ordinal numbers (see Unit [Ordinal Numbers – in preparation]). Here we only present some elementary properties.
Definition. Let $(A, \leq)$ be an ordered set, and let $a$ be an element of the set $A$. Then the set
$$
A_a := \{x \in A \mid x < a \}
$$
is called the initial segment of the set $A$ with respect to the element $a$.
French / German. Initial segment = Section commençante (or Segment initial) = Anfangsstück.
Definition. Let $A = (A, \leq)$ be an ordered set, and let $a$ be an element of the set $A$. Then the set
$$
T_a := \{ x \in A \mid x \geq a \}
$$
is called the final segment of the set $A$ with respect to the element $a$.
French / German. Final segment = Section finissante = Endstück
Proposition. Let $A$ be a totally ordered set, let $a$ be an element of the set $A$, and let
$A_a := \{ x \in A \mid x < a \}$ and $T_a := \{ x \in A \mid x \geq a \}$
be the initial and the final segment with respect to the element $a$.

(a) We have $A = A_a \mathbin{\dot{\cup}} T_a$.
(b) We have $\big( A_a \big)^c = T_a$ (complement of the set $A_a$ in the set $A$).
(c) We have $\big( T_a \big)^c = A_a$ (complement of the set $T_a$ in the set $A$).
Chains of Ordered Sets
Definition. Let $I$ be a totally ordered index set. A family $(A_i, \leq_i)_{i \in I}$ is called a chain of ordered sets if the following conditions are fulfilled:
(i) The family $(A_i)_{i \in I}$ is a chain, that is, we have $A_i \subseteq A_j$ whenever $i \leq j$.
(ii) For each two elements $i$ and $j$ of the set $I$ such that $i \leq j$, the order $\leq_i$ on the set $A_i$ is induced by the order $\leq_j$ on the set $A_j$, that is, we have
$$
x \leq_i y \mbox{ if and only if } x \leq_j y \mbox{ for all } x, y \in A_i.
$$
French / German. Chain of ordered sets = Chaîne d’ensembles ordonnés = Kette geordneter Mengen.
Theorem. Let $I$ be a totally ordered index set, let $(A_i, \leq_i)_{i \in I}$ be a chain of ordered sets, and let $A := \bigcup_{i \in I} A_i$.

(a) There exists exactly one order $\leq_A$ on the set $A$ such that for all elements $i$ of the set $I$ we have
$$
x \leq_A y \mbox{ if and only if } x \leq_i y \mbox{ for all } x, y \in A_i,
$$
that is, the orders $\leq_i$ are induced by the order $\leq$ for all elements $i$ of the set $I$.
(b) If we have $A = A_i$ for an element $i$ of the set $I$, then we have $(A, \leq_A) = (A, \leq_i)$.
Theorem [#nst-th-ordered-chain-order-union] allows to replace a chain of ordered sets by one ordered set.
Definition. Let $I$ be a totally ordered index set, let $(A_i, \leq_i)_{i \in I}$ be a chain of ordered sets, and let $A := \bigcup_{i \in I} A_i$.
The order $\leq_A$ on the set $A$ defined in Theorem [#nst-th-ordered-chain-order-union] is called the order of the set $A = \bigcup_{i \in I} A_i$ induced by the chain of ordered sets $(A_i, \leq_i)_{i \in I}$.
French / German. Order induced by a chain of ordered sets = Ordre induit par une chaîne d’ensembles ordonnés = Durch eine Kette geordneter Mengen induzierte Ordnung.
The Lemma of Zorn
The Lemma of Zorn is a powerful tool to prove the existence of maximal elements in partially ordered sets. It is a consequence of the axiom of choice which has been explained in Unit Families and the Axiom of Choice.
Theorem. (Lemma of Zorn – Special Case) Let $S$ be a non-empty set, and consider the ordered set ${\cal P}(S) = \big( {\cal P}(S), \subseteq \big)$ where ${\cal P}(S)$ denotes the power set of the set $S$. Let
$$
\emptyset \neq {\cal D} \subseteq {\cal P}(S)
$$
be a non-empty set of subsets of the set $S$ such that for each chain ${\cal C}$ in the set ${\cal D}$ the set
$$
Z := \bigcup_{X \in {\cal C}} X
$$
is also an element of the set ${\cal D}$.
Then the set ${\cal D} = \big( {\cal D}, \subseteq \big)$ contains a maximal element.
Definition. Let $A = (A, \leq)$ be an ordered set, and let $B$ be a subset of the set $A$.
(a) An element $a$ of the set $A$ is called an upper bound of the set $B$ if we have
$x \leq a$ for all $x \in B$ comparable to $a$.
(b) An element $a$ of the set $A$ is called a lower bound of the set $B$ if we have
$a \leq x$ for all $x \in B$ comparable to $a$.
French / German. Upper bound = Majorant = Obere Schranke. Lower bound = Minorant = Untere Schranke.
Theorem. (Lemma of Zorn – General Case) Let $A = (A, \leq)$ be an ordered set such that every chain $C$ of the set $A$ has an upper bound in the set $A$.
Then the set $A$ contains a maximal element.
Notes and References
A list of textbooks about set theory is contained in Unit [Literature about Set Theory].
Do you want to learn more? We will close the list of the axioms of Zermelo and Fraenkel by explaining the last axiom, the axiom of infinity, in Unit Successor Sets and the Axioms of Peano.
Download
Ordered Sets and the Lemma of Zorn
Ordered Sets and the Lemma of Zorn:
The pdf document is the full text including the proofs.
Current Version: 1.0.3 from October 2020
