Functions and Equivalent Sets
- Introduction
- Functions
- Injective, Surjective and Bijective Functions
- The Composition of Functions
- Restrictions and Extensions of Functions
- Functions and Equivalence Relations
- Equivalent Sets
- Notes and References
- Download
Introduction
In the following you will find a short summary of this unit. For detailed information please see the full text or download the pdf document at the end of this page.
The present unit is the fourth unit of the walk The Axioms of Zermelo and Fraenkel. Based on the relations introduced in Unit Direct Products and Relations we will introduce functions as specific relations:
We will explain the following terms:
- Function
- Graph of a Function
- Domain, Codomain, Range and Image of a Function
- Inverse Image of a Function
- Identity Function and Inclusion Map
- Injective, Surjective and Bijective Functions
- Composite of two Functions
- Inverse Function
- Group, Commutative or Abelian Group
- Restriction and Extension of a Function
- Well defined Function
- Equivalent Sets
You will learn the main results of this unit:
- Theorem [#nst-th-function-identical] saying that two functions $f : A \rightarrow B$ and $g : A \rightarrow B$ are equal if and only if $f(x) = g(x)$ for all elements $x$ of the set $A$,
- Theorem [#nst-th-bijective-functions-group] saying that the set of the bijective functions $f : A \rightarrow A$ from a set $A$ onto itself forms a group and
- Theorem [#nst-th-making-one-set-disjoint] saying that for two arbitrary sets $A$ and $B$ there exists always a set $B’$ equivalent to the set $B$ such that $A \cap B’ = \emptyset$.
Functions
The definition of a function will be based on direct products and relations explained in Unit Direct Products and Relations:
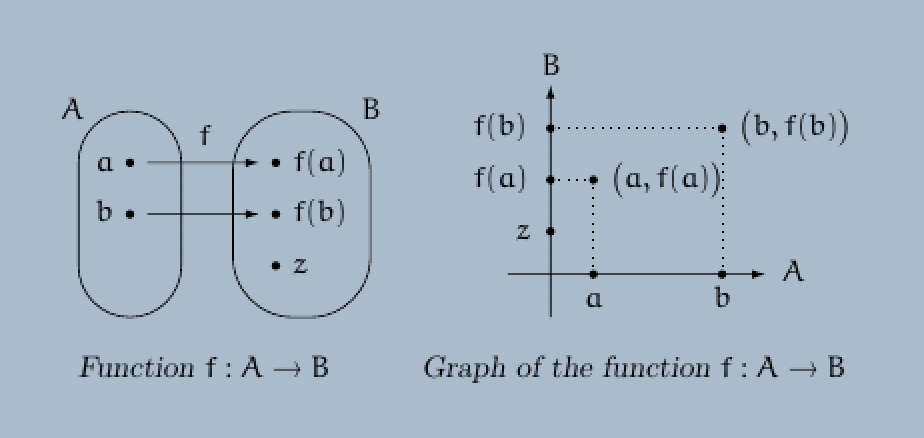
Definition. Let $A$ and $B$ be two sets.
(a) A function $f : A \rightarrow B$ from the set $A$ into the set $B$ is a triple $(f, A, B)$ where the set $f$ is a subset of the direct product $A \times B$ with the following property:
For each element $x$ of the set $A$, there is exactly one element $y$ of the set $B$ such that the pair $(x, y)$ is contained in the set $f$.
A function $f : A \rightarrow B$ from the set $A$ into the set $B$ is also called a mapping from the set $A$ into the set $B$ or a transformation from the set $A$ into the set $B$.
(b) Let $f : A \rightarrow B$ be a function from the set $A$ into the set $B$, and let $x$ be an element of the set $A$. The unique element $y$ of the set $B$ such that the pair $(x, y)$ is contained in the set $f$ is denoted by $y = f(x)$. We also write $f : x \mapsto y$ or, equivalently, $f : x \mapsto f(x)$.
(c) Let $f : A \rightarrow B$ be a function from the set $A$ into the set $B$. Then the set
$$
G_f := \{ \big(x, f(x) \big) \in A \times B \mid x \in A \}
$$
is called the graph of the function $f$.
French / German. Function = Fonction = Funktion. Mapping = Application = Abbildung. Graph = Graphe = Graph.
Theorem. Let $A$ and $B$ be two sets, and let $f : A \rightarrow B$ and $g : A \rightarrow B$ be two functions from the set $A$ into the set $B$.
Then we have $f = g$ if and only if $f(x) = g(x)$ for all elements $x$ of the set $A$.
Definition. Let $f : A \rightarrow B$ be a function from a set $A$ into a set $B$.
(a) The set $A$ is called the domain of the function $f$, and the set $B$ is called the codomain of the function $f$.
(b) The set
$$
R := \{ f(x) \mid x \in A \} \subseteq B
$$
is called the range of the function $f$ or, equivalently, the image of the function $f$. We also write $R = f(A)$ or $R = \mbox{Image } f$. (Sometimes the word range is also used in the meaning of the codomain.)
(c) Let $X$ be a subset of the set $A$. Then the set
$$
Y := \{ f(x) \mid x \in X \} \subseteq B
$$
is called the image of the set $X$ under the function $f$. We also write $Y = f(X)$.
French / German. Domain = Domaine de définition = Definitionsbereich; Codomain = Codomaine = Wertebereich; Image (or range) = Imâge = Bild.
Definition. Let $f : A \rightarrow B$ be a function from a set $A$ into a set $B$, and let $Y$ be a subset of the set $B$. We set
$$
f^{-1}(Y) := \{ x \in A \mid f(x) \in Y \} \subseteq A.
$$
The set $f^{-1}(Y)$ is called the inverse image of the set $Y$ under the function $f$.
French / German. Inverse Image = Imâge réciproque = Urbild.
Definition. (a) Let $A$ be a set, and let $f : A \rightarrow A$ be the function defined by
$$
f(x) := x \mbox{ for all } x \in A
$$
or, equivalently, by
$$
f := \{ (x, y) \in A \times A \mid y = x \} = \{ (x, x) \in A \times A \mid x \in A \}.
$$
The function $f : A \rightarrow A$ is called the identity function on the set $A$.
It is denoted by $\mbox{id}_A : A \rightarrow A$ or, equivalently, by $\mbox{id} : A \rightarrow A$ if no confusion may arise.
Note that $\mbox{id} = \emptyset$ if $A = \emptyset$.
(b) Let $B$ be a set, let $A$ be a subset of the set $B$, and let $g : A \rightarrow B$ be the function defined by
$$
g(x) := x \mbox{ for all } x \in A
$$
or, equivalently, by
$$
g := \{ (x, y) \in A \times B \mid y = x \} = \{ (x, x) \in A \times B \mid x \in A \}.
$$
The function $g : A \rightarrow B$ is called the inclusion map or, equivalently, the inclusion function.
It is denoted by $\iota : A \rightarrow B$ or, equivalently, by $A \hookrightarrow B$.
French / German. Identity = Identité = Identität.
Injective, Surjective and Bijective Functions
The terms injective, surjective and bijective play an important role for the investigation of functions:
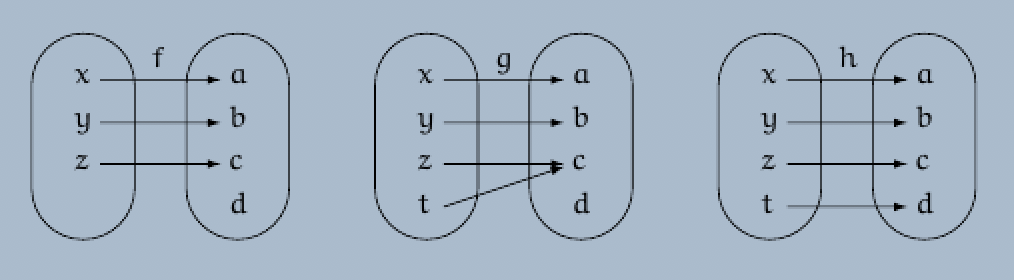
Definition. Let $A$ and $B$ be two sets, and let $f : A \rightarrow B$ be a function from the set $A$ into the set $B$.
(a) The function $f : A \rightarrow B$ is called injective if $f(x) \neq f(x’)$ for each two elements $x$, $x’$ of the set $A$ such that $x \neq x’$.
(b) The function $f : A \rightarrow B$ is called surjective if for each element $y$ of the set $B$ there exists an element $x$ of the set $A$ such that $f(x) = y$.
(c) The function $f : A \rightarrow B$ is called bijective if $f$ is injective and surjective.
French / German. Injective = Injective = Injektiv. Surjective = Surjective = Surjektiv. Bijective = Bijective = Bijektiv.
The Composition of Functions
The most important result of this sections is that the set of the bijective functions $f : A \rightarrow A$ from a set $A$ into itself forms a group with respect to the composition of functions.
Definition. Let $A$, $B$ and $C$ be three sets, and let $f : A \rightarrow B$ and $g : B \rightarrow C$ be two functions from the set $A$ into the set $B$ and from the set $B$ into the set $C$, respectively.
Define the function $h : A \rightarrow C$ by $h(x) := g \big( f(x) \big)$ for all elements $x$ of the set $A$.
(a) The function $h : A \rightarrow C$ is called the composite of the two functions $f : A \rightarrow B$ and $g : B \rightarrow C$.
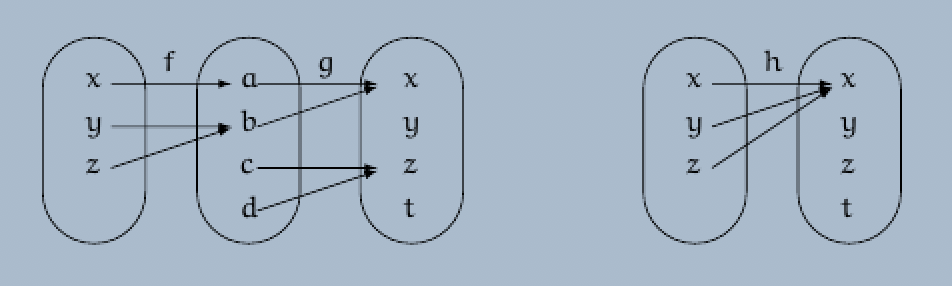
(b) The function $h : A \rightarrow C$ is denoted by $g \circ f : A \rightarrow C$.
French / German. Composition of two functions = Composition de deux fonctions = Verkettung / Hintereinanderausführung von zwei Funktionen.
Proposition. Let $A$, $B$ and $C$ be three sets, and let $f : A \rightarrow B$ and $g : B \rightarrow C$ be two functions from the set $A$ into the set $B$ and from the set $B$ into the set $C$, respectively.
(a) If the functions $f : A \rightarrow B$ and $g : B \rightarrow C$ are injective, then the function $g \circ f : A \rightarrow C$ is also injective.
(b) If the functions $f : A \rightarrow B$ and $g : B \rightarrow C$ are surjective, then the function $g \circ f : A \rightarrow C$ is also surjective.
(c) If the functions $f : A \rightarrow B$ and $g : B \rightarrow C$ are bijective, then the function $g \circ f : A \rightarrow C$ is also bijective.
Definition. Let $A$ and $B$ be two sets, and let $f : A \rightarrow B$ be a bijective function. We define the function $g : B \rightarrow A$ as follows: For each element $y$ of the set $B$, let $x$ be the unique element of the set $A$ such that $f(x) = y$. Set $g(y) := x$.
The function $g : B \rightarrow A$ is called the inverse function of the function $f : A \rightarrow B$. It is denoted by $f^{-1} : B \rightarrow A$.
French / German. Inverse function = Fonction inverse = Inverse Funktion.
Definition. (a) A pair $(G, *)$ consisting of a non-empty set $G$ and an operation
$$
* : G \times G \rightarrow G
$$
on the set $G$ is called a group if the following conditions are fulfilled:
(i) We have
$$
x * y \in G \mbox{ for all } x, y \in G \mbox{ (closure)}.
$$
(ii) We have
$$
(x * y) * z = x * (y * z) \mbox{ for all } x, y, z \in G \mbox{ (associativity)}.
$$
(iii) There exists an element $id$ of the group $G$ such that
$$
x * id = id * x = x \mbox{ for all } x \in G \mbox{ (existence of an identity element)}.
$$
(iv) For each element $x$ of the group $G$, there exists an element $y = y_x$ of the group $G$ such that
$$
x * y = id \mbox{ (existence of an inverse element)}.
$$
The element $y$ is denoted by $x^{-1}$.
(b) If the pair $(G, *)$ is a group, we often just say that $G$ is a group or that $G = (G, *)$ is a group.
(c) A group $G = (G, *)$ is called a commutative group or, equivalently, an abelian group if we have
$$
x * y = y * x\mbox{ for all } x, y \in G.
$$
French / German. Group = Groupe = Gruppe. Commutative = Commutatif = Kommutativ. Abelian = Abélien = Abelsch.
Theorem. Let $A$ be a set, and let
$$
{\cal B}(A) := \{ f : A \rightarrow A \mid f \mbox{ is bijective} \}
$$
be the set of the bijective functions from the set $A$ into itself.
Then the pair $\big( {\cal B}(A), \circ \big)$ is a group where $\circ$ denotes the composition of two functions of the set ${\cal B}(A)$. In general, this group is not abelian.
Restrictions and Extensions of Functions
Given a function $f : A \rightarrow B$ from a set $A$ into a set $B$ it is often useful to restrict the function $f$ to a function $f : A_1 \rightarrow B$ with $A_1 \subseteq A$ or to extend the function $f$ to a function $f : A_2 \rightarrow B$ with $A \subseteq A_2$. In this unit we only look at the basic definition. This topic becomes more interesting when investigating functions with specific properties such as continuous or holomorphic functions.
Definition. Let $f : A \rightarrow B$ and $g : A’ \rightarrow B’$ be two functions from a set $A$ into a set $B$ and from a set $A’$ into a set $B’$, respectively. Suppose that the sets $A’$ and $B’$ are subsets of the sets $A$ and $B$, respectively.
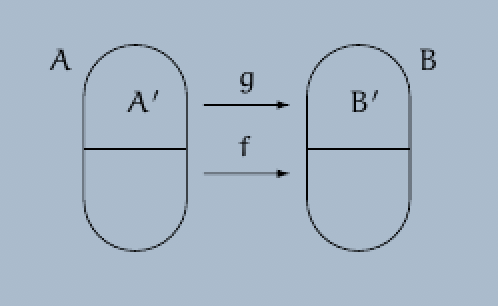
We say that the function $g : A’ \rightarrow B’$ is a restriction of the function $f : A \rightarrow B$ or, equivalently, that the function $f : A \rightarrow B$ is an extension of the function $g : A’ \rightarrow B’$ or, equivalently, that the function $g : A’ \rightarrow B’$ is induced by the function $f : A \rightarrow B$ if we have
$$
f(x) = g(x) \mbox{ for all } x \in A’.
$$
In this case we write $g = f|_{A’} : A’ \rightarrow B’$.\index{$f_A : A \rightarrow B$}
French / German. Restriction = Restriction = Einschränkung. Extension = Prolongement = Fortsetzung. Induced by = Induit par = Induziert von.
Proposition. Let $A_1$, $A_2$, $B_1$ and $B_2$ be four non-empty sets, and let $f_1 : A_1 \rightarrow B_1$ and $f_2 : A_2 \rightarrow B_2$ be two functions of the sets $A_1$ and $A_2$ into the sets $B_1$ and $B_2$, respectively.
Suppose that $f_1(x) = f_2(x)$ for all elements $x$ of the set $A_1 \cap A_2$. Note that this implies that $f_1(x) = f_2(x) \in B_1 \cap B_2$ for all $x \in A_1 \cap A_2$.
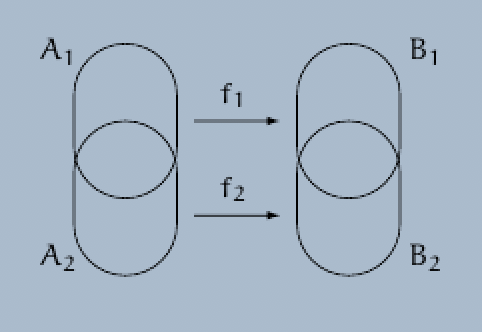
(a) There exists exactly one function $f : A_1 \cup A_2 \rightarrow B_1 \cup B_2$ such that $f|_{A_1} = f_1$ and $f|_{A_2} = f_2$.
(b) If the functions $f_1 : A_1 \rightarrow B_1$ and $f_2 : A_2 \rightarrow B_2$ are surjective, then the function $f : A_1 \cup A_2 \rightarrow B_1 \cup B_2$ is also surjective.
Proposition. Let $A_1$, $A_2$, $B_1$ and $B_2$ be four non-empty sets such that $A_1 \cap A_2 = \emptyset$ and $B_1 \cap B_2 =\emptyset$, and let $f_1 : A_1 \rightarrow B_1$ and $f_2 : A_2 \rightarrow B_2$ be two functions of the sets $A_1$ and $A_2$ into the sets $B_1$ and $B_2$, respectively.
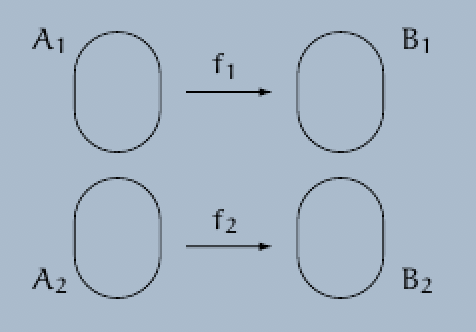
(a) There exists exactly one function $f : A_1 \cup A_2 \rightarrow B_1 \cup B_2$ such that $f|_{A_1} = f_1$ and $f|_{A_2} = f_2$.
(b) If the functions $f_1 : A_1 \rightarrow B_1$ and $f_2 : A_2 \rightarrow B_2$ are injective, then the function $f : A_1 \cup A_2 \rightarrow B_1 \cup B_2$ is also injective.
(c) If the functions $f_1 : A_1 \rightarrow B_1$ and $f_2 : A_2 \rightarrow B_2$ are surjective, then the function $f : A_1 \cup A_2 \rightarrow B_1 \cup B_2$ is also surjective.
(d) If the functions $f_1 : A_1 \rightarrow B_1$ and $f_2 : A_2 \rightarrow B_2$ are bijective, then the function $f : A_1 \cup A_2 \rightarrow B_1 \cup B_2$ is also bijective.
Functions and Equivalence Relations
In the present section we will explain the relation between functions and equivalence relations. Equivalence relations have been explained in Unit Direct Products and Relations.
Definition. Let $f : A \rightarrow B$ be a function from a set $A$ into a set $B$, and let $\sim$ be an equivalence relation on the set $A$. For an element $x$ of the set $A$, let $\bar{x} := \{ z \in A \mid z \sim x \}$ be the equivalence class defined by the element $x$.
The function $\alpha : \bar{A} \: \rightarrow B$ from the set $\bar{A}$ of the equivalence classes of the set $A$ into the set $B$ defined by $\alpha : \bar{x} \mapsto f(x)$ is called well defined if we have
$$
f(x) = f(y) \mbox{ for all } x, y \in A \mbox{ with } x \sim y.
$$
French / German. Well defined = Bien défini = Wohldefiniert.
Proposition. Let $f : A \rightarrow B$ be a function from a set $A$ into a set $B$. For two elements $x$ and $y$ of the set $A$, set
$$
x \sim y \mbox{ if and only if } f(x) = f(y).
$$
(a) The relation $\sim$ is an equivalence relation on the set $A$.
(b) For an element $x$ of the set $A$, let $\bar{x} := \{ z \in A \mid z \sim x \}$ be the equivalence class defined by the element $x$.
Then the function $\alpha : \bar{A} \: \rightarrow B$ from the set $\bar{A}$ of the equivalence classes of the set $A$ into the set $B$ defined by $\alpha : \bar{x} \mapsto f(x)$ is well defined and injective.
Equivalent Sets
Equivalent sets play an important role for the definition of the cardinality of a set.
Definition. Two sets $A$ and $B$ are called equivalent if there exists a bijective function $f : A \rightarrow B$ from the set $A$ onto the set $B$. If the sets $A$ and $B$ are equivalent, we write $A \sim B$.
French / German. Equivalent = Équivalent = Äquivalent.
Proposition. Let $A$, $B$ and $C$ be three sets.
(a) We have $A \sim A$ (reflexivity).
(b) If $A \sim B$, then we have $B \sim A$ (symmetry).
(c) If $A \sim B$ and $B \sim C$, then we have $A \sim C$ (transitivity).
Theorem. Let $A$ and $B$ be two non-empty sets. Then there exists a set $B’$ fulfilling the following conditions:
(i) The sets $B$ and $B’$ are equivalent.
(ii) We have $A \cap B’ = \emptyset$.
Notes and References
A list of textbooks about set theory is contained in Unit [Literature about Set Theory].
Do you want to learn more? In Unit Families and the Axiom of Choice we will explain how to define families $(A_i)_{i \in I}$ in the context of the axioms of Zermelo and Fraenkel, and we will explain the famous axiom of choice.
Download
Functions and Equivalent Sets
The pdf document is the full text including the proofs.
Current Version: 1.0.3 from October 2020
