
Direct Products and Relations
- Introduction
- Ordered Pairs
- The Direct Product of Two Sets
- Relations
- Equivalence Relations and Partitions
- Notes and References
- Download
Introduction
In the following you will find a short summary of tis unit. For detailed information please see the full text or download the pdf document at the end of this page.
The present unit is the third unit of the walk The Axioms of Zermelo and Fraenkel. In the previous units The Mathematical Universe and Unions and Intersections of Sets we have introduced the basic axioms of Zermelo and Fraenkel.
We will explain the following terms:
- Ordered Pair
- Direct Product
- Relation
- Reflexive, symmetric, antisymmetric and transitive relation
- Equivalence Relation
- Partition
The main results are
- Theorem [#nst-th-ordered-pair-elementary] about ordered pairs saying that we have $(a, b) = (a’, b’)$ if and only if $a = a$ and $b = b’$ and
- Theorem [#nst-th-equivalence-relation-partition] saying that each equivalence relation defines a partition and that each partition defines an equivalence relation.
Ordered Pairs
We will introduce the definition of ordered pairs:
Definition. Let $a$ and $b$ be two sets.
The ordered pair $(a, b)$ is defined by $(a, b) := \big\{ \{a\}, \{a, b\} \big\}$.
French / German. Ordered pair = Paire ordonnée = Geordnetes Paar.
Theorem. Let $a$ and $b$ be two sets.
(a) If $a = b$, then we have $(a, b) = (a, a) = \big\{ \{a\} \big\}$.
(b) If $a \neq b$, then we have $(a, b) \neq (b, a)$.
(c) Let $a$, $a’$, $b$ and $b’$ be four sets. Then we have $(a, b) = (a’, b’)$ if and only if $a = a’$ and $b = b’$.
(d) Suppose that the sets $a$ and $b$ are elements of the sets $A$ and $B$, respectively. Then the ordered pair $(a, b)$ is an element of the set ${\cal P} \big( {\cal P} (A \cup B) \big)$.
The Direct Product of Two Sets
The direct product of two sets is one of the basic tools in mathematics such as the union or the intersection of two sets.
Definition. Let $A$ and $B$ be two sets. Set
$$
A \times B := \{ x \in {\cal P} \big( {\cal P} (A \cup B) \big) \mid \exists \: a \in A \: \exists \: b \in B \mbox{ s.t. } x = (a, b) \}.
$$
(a) The set $A \times B$ is called the direct product of the sets $A$ and $B$ or, equivalently, the Cartesian product of the sets $A$ and $B$.
(b) We write $A \times B := \{ (a, b) \mid a \in A \mbox{ and } b \in B \}$ for short.
French / German. Direct product = Produit direct = Direktes Produkt.
Proposition. Let $A$, $B$, $C$ and $D$ be four sets.
(a) We have $(A \cup B) \times C = (A \times C) \cup (B \times C)$.
(b) We have $(A \cap B) \times C = (A \times C) \cap (B \times C)$.
(c) We have $(A \cap B) \times (C \cap D) = (A \times C) \cap (B \times D) = (A \times D) \cap (B \times C).$
(d) We have $(A \cup B) \times (C \cup D) = (A \times C) \cup (A \times D) \cup (B \times C) \cup (B \times D).$
(e) We have $(A \setminus B) \times C = (A \times C) \setminus (B \times C)$.
Relations
Relations are used to express a connection between two mathematical objects. Particularly important relations are equivalence relations (see below), functions (see Unit Functions and Equivalent Sets) and order relations (see Unit Ordered Sets and the Lemma of Zorn).
Definition. Let $A$ and $B$ be two sets.
(a) Every subset $R$ of the direct product $A \times B$ is called a relation on the direct product $A \times B$. More precisely, the set $R$ is called a binary relation.
(b) If $A = B$, a relation $R$ on the direct product $A \times B = A \times A$ is called a relation on the set $A$.
(c) Let $R \subseteq A \times B$ be a relation. Two elements $a$ of the set $A$ and $b$ of the set $B$ are called related with respect to the relation $R$ if the pair $(a, b)$ is contained in the set $R$.
If the elements $a$ and $b$ are related with respect to the relation $R$, we write $a \: R \: b$.
(d) Often we denote a relation $R$ by a symbol like $*$ or $\sim$. We then speak of the relations $*$ or $\sim$, and we write $x * y$ or $x \sim y$ if the elements $x$ and $y$ are related with respect to the relation $*$ or $\sim$, respectively.
French / German. Relation = Relation = Relation.
Definition. Let $A$ be a set, and let $*$ be a relation on the set $A$.
(a) The relation $*$ is called reflexive if we have $x * x$ for all elements $x$ of the set $A$.
(b) The relation $*$ is called symmetric if we have $x * y$ if and only if $y * x$ for all elements $x$ and $y$ of the set $A$.
(c) The relation $*$ is called antisymmetric if $x * y$ and $y * x$ imply $x = y$ for all elements $x$ and $y$ of the set $A$.
(d) The relation $*$ is called transitive if for each three elements $x$, $y$ and $z$ of the set $A$ the relations $x * y$ and $y * z$ imply $x * z$.
French / German. Reflexive = Réflexive = Reflexif; Symmetric = Symétrique = Symmetrisch; Antisymmetric = Antisymétrique = Antisymmetrisch; Transitive = Transitive = Transitif.
Equivalence Relations and Partitions
Equivalence relations are used to group and often to identify similar elements of a set:
Definition. Let $A$ be a non-empty set, and let $\sim$ be a relation on the set $A$.
(a) The relation $\sim$ is called an equivalence relation if it is reflexive, symmetric and transitive.
(b) Let $\sim$ be an equivalence relation, and let $x$ be an element of the set $A$. The set
$$
A_x := \{ y \in A \mid y \sim x \}
$$
is called an equivalence class with respect to the equivalence relation $\sim$.
(c) The quotient of the set $A$ with respect to the equivalence relation $\sim$ is the set
$$
\bar{A} := \{ A_x \mid x \in A \}.
$$
It is denoted by $\bar{A}$ or by $A / \sim$. The elements $A_x$ of the set $\bar{A} = A / \sim$ often are denoted by $\bar{x} := A_x$. We have
$$
\bar{A} = \{ \bar{x} \mid x \in A \}.
$$
French / German. Equivalence relation = Relation d’équivalence = Äquivalenzrelation.
Proposition. Let $A$ be a set, and let $\sim$ be an equivalence relation on the set $A$. Let $x$ and $y$ be two elements of the set $A$, and let $A_x$ and $A_y$ be the equivalence classes of the elements $x$ and $y$, respectively.
(a) The element $x$ is contained in the set $A_x$.
(b) We have $x \sim y \mbox{ if and only if } A_x = A_y.$
(c) We have $A_x = A_y$ or $A_x \cap A_y = \emptyset$.
(d) We have $A = \bigcup_{x \in A} A_x$.
Definition. Let $A$ be a non-empty set, and let ${\cal C}$ be a set of non-empty subsets of the set $A$.
(a) The set ${\cal C}$ is called a partition of the set $A$ if the following conditions are fulfilled:
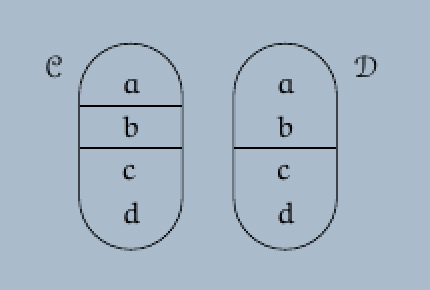
(i) We have $\bigcup_{C \in {\cal C}} C = A$.
(ii) We have $C \cap D = \emptyset$ for all elements $C$ and $D$ of the set ${\cal C}$ such that $C \neq D$.
(b) The union $A = \bigcup_{C \in {\cal C}} C$ is called a disjoint union.
French / German. Partition = Partition = Partition. Disjoint Union = Union disjointe = Disjunkte Vereinigung.
Theorem. Let $A$ be a non-empty set.
(a) Let $\sim$ be an equivalence relation on the set $A$. Then the equivalence classes of the set $A$ with respect to the relation $\sim$ form a partition of the set $A$.
(b) Let ${\cal C}$ be a partition of the set $A$. For two elements $x$ and $y$ of the set $A$, define $x \sim y$ if and only if there exists an element $C$ of the partition ${\cal C}$ containing both elements $x$ and $y$.
Then the relation $\sim$ is an equivalence relation on the set $A$.
The equivalence classes of the relation $\sim$ are exactly the sets of the partition ${\cal C}$.
Notes and References
A list of textbooks about set theory is contained in Unit [Literature about Set Theory].
Do you want to learn more? In the framework of the axioms of Zermelo and Fraenkel functions are defined as relations with specific properties. This approach is explained in Unit Functions and Equivalent Sets.
Download
Direct Products and Relations
The pdf document is the full text including the proofs.
Current Version: 1.0.3 from October 2020
